



Perpetual Fragility
Perpetual Fragility is a small Commodore 64 demo that I wrote for the snowstorm compo at Fjälldata 2023. Here's an explanation of how it works.
Download
- lft-perpetual-fragility.prg (Demo, C64 executable, 9.2 kB)
- lft-pf-254bytes-full.prg (Music, C64 executable, 254 bytes)
- lft-pf-254bytes-compo-edit.prg (Music, shortened version, C64 executable, 254 bytes)
- Linus Akesson - Perpetual Fragility.mp3 (MP3, 8.2 MB)
CSDb pages for the demo and the standalone music release.
Introduction
Demos, like other works of art, can be appreciated for their aesthetic qualities. But for an oldschool demo platform such as the Commodore 64, where the hardware places a lot of restrictions on what you can display on the screen, there is an extra dimension: An effect can be impressive because it seems to do something impossible. And just as when you're watching a magic trick, half the fun is trying to figure out how it was pulled off.
On a modern computer, a straightforward way to implement a snowstorm effect would be to, for each video frame, clear a framebuffer (a sort of canvas in memory), simulate the movement of every snowflake, and then draw them into the buffer. But on a C64 with less than 20,000 clock cycles available per video frame, there wouldn't even be enough time for the CPU to clear the framebuffer, let alone compute new coordinates for a thousand snowflakes. Clearly, we can rule out realtime number crunching.
A pre-rendered video is also out of the question. With a total of 64 KB of RAM, the C64 cannot hold more than a handful of full-screen images in memory.
And yet we somehow see more than a thousand dots dancing around on the screen, and the effect seems to be running smoothly at full framerate. If it's neither realtime-rendered nor offline-rendered, what sorcery are we looking at? If you're a C64 coder and you want to crack this mystery on your own, now is the time to stop reading. The rest of you, stay tuned and I'll reveal exactly how it works!
The music
The composition is inspired by the works of Arvo Pärt. You are encouraged to listen carefully, as there are patterns and structures to discover.
In part because of these structures, the music can be generated by a very small piece of code. The standalone music player occupies only 254 bytes, exactly one disk block in Commodore DOS. But from a technical point of view it's pretty similar to what I did in A Mind Is Born, so I won't delve into the details of the playroutine here.
Setting the stage
Like many magic tricks, what looks simple, slick, and impossible on the outside can be unglamorous and rather complicated behind the curtain. But I think there's a certain elegance in this one.
We'll start with the basics: The Commodore 64 Programmer's Reference Guide tells us that the C64 has two distinct video modes: Text and bitmap graphics. Text mode displays a grid of 40x25 characters from a user-definable font. The characters can consist of 8x8 high-resolution pixels or 4x8 low-resolution (wide) pixels; in the latter case the characters can be more colourful. Bitmap mode can be used to display a static picture.
We also learn that we can place eight small movable objects—MOBs or sprites—in front of or behind the main graphics (the text or bitmap). And by updating the sprite control registers in realtime while a video frame is being generated (from top to bottom), we can reuse the sprite hardware and thus have more than eight sprites visible on the screen—but never more than eight side by side on the same rasterline.
These are the building blocks, the clay that C64 coders have been shaping into demo parts for four decades.
Sprites
When we look at this particular effect, it would seem reasonable at first to assume that the snowflakes are sprites, since they are small objects moving in front of a static background. But the candle and flame concentrate a whole bunch of different colours in high-resolution pixels in a small area, so they must be sprites. And with all those colours, the flame will hog most of the sprite hardware on those particular rasterlines. We don't see a corresponding reduction in the number of snowflakes around that Y-position; they fill the screen pretty evenly. But we do see a lack of detail and breadth in the tree next to the candle. This reveals that the tree, candle, and flame are sprites while the snowflakes are rendered by the main graphics generator. The frost along the edge of the window is also sprites.
The tree is built up from a combination of high-resolution (“-”) and X-expanded (“=”) sprites, like this:
1f 20 **** 21 -------------------**### ------------------------------------------------ 22 ------------------*###-- ------------------------------------------------ 23 -**--------------*##---- ------------------------------------------------ 24 -#******-------**##----- ------------------------------------------------ 25 -##*####-------*###----- ------------------------------------------------ 26 -#####--------*###------ ------------------------------------------------ 27 --###--------*###------- ------------------------------------------------ 28 --###*------**###------- -------------------------**--------------------- 29 ---###**---**####*------ ------------------------*##--------------------- 2a ---####******#####------ ------------------------###------------------**- 2b ----########*#####*----- -----------------------*###-----------------*### 2c -----##############*---- -----------------------###-----------*-----*###- 2d -------############*---- -----------------------###*--------**#-----*###- 2e ------------########---- -----------------------####-------*###----*###-- 2f ---------------#####*--- ----------------------*####------*####---*####-- 30 ----------------#####*-- -***------------------####-----**####****####--- 31 -----------------####*-- -###*----------------*###--****####**#######---- 32 ------------------####*- *####*--------------*####**################----- 33 ------------------#####* ######--------------#####################------- 34 -------------------####* ##-###*------------*###################--------- 35 -------------------#####* ----###------------########---##---------------- 36 ------------------------ -#####------------------============================##============###### ------------------------ 37 ------------------------ -#####*--------*--------============================##============###### ------------------------ 38 ------------------------ --#####*-------#*-------============================##==========**####== ------------------------ 39 ------------------------ ---####*-------##**-----============================##==========######== ------------------------ 3a ------------------------ ---#####*------####*----============================##==========######== ------------------------ 3b ------------------------ ----#####-------####*---============================##========**######== ------------------------ 3c -------*---------------- ----#####*--------##*---============================##********######==== ------------------------ 3d -----**#*--------------- -----####*--------###**-==**====================**********##########==== ----------------------** 3e -----####**------------- -----#####---------####***##****======************################====== ---------------------*## 3f -------####**----------- -----#####*---------############********########################======== --------------------*##- 40 --------#####*--*------- ------#####--------*########################################============ -------------------*##-- 41 ---------#####--#*------ ------#####--------*##########################################========== ----------------***##--- 42 -----------###*-##*----- ----**#####--------##############################===##======##========== ----------------####---- 43 -----------####--##----- ----#*#####--------#######################==========##================== ---------------*###----- 44 ------*----####**##----- ----#######*------*#############====================##================== ------------***###------ 45 -----*#-----#######**--- -----######*-----*########==========================##**================ ----------**######------ 46 -----##*----#########*-- ------######*****#######==========================**####================ -----*****########------ 47 ----*###---*##########-- ------#######**########-==========================######================ ---**##########--------- 48 --**####***####-######*- -------################-==========================####========**======== --*##########----------- 49 -*###########----######* -------###############--========================**####======**##======== -*#######--------------- 4a *###---###--------**#### --------##############--========================####========##========== -#####------------------ 4b ##============****######**====================== ====############========================**####====**==##==============================================================**####==================== 4c ==============############**==================== ====############========================######====##**##==========================================================**==######==================== 4d ================####==######==================== ==**############========================######==**######**========================================================##**####====================== 4e ======================######**================== ==##############==========================####**##########========================================================########====================== 4f ======================########================== ==##############==========================####**######==========================================================**######======================== 50 ========================######**================ ==##==##########==========================##########==========================================================**########======================== 51 ========================########================ ======##########==========================########==========================================================**########========================== 52 ==========================######================ ======##########**========================########==========================================================########============================ 53 ============================####**============== ======############======================**######============================================================########============================ 54 ============================######============== ======############======================########============================================================######============================== 55 ============================######**============ ========##########==================****########==========================================================**####==================**============ 56 ==============================####****========== ========##########==================##########============================================================######==================##****======== 57 ==============================########========== ========########==================**##########==========================================================**####================****######======== 58 ==============================########******==== ========########==================##########==========================================================**######================########========== 59 ================================############**== ========########==================########====================================================**==****######================**########========== 5a ================================############==== ========########==================########==================================**==============**##**##########================######============== 5b ================================##########====== ========########====================######==================================##============**##############================**####================ 5c ==================================########**==== ==========######====================######============================**==**##============##############================**######================ 5d ==================================##########**== ==========######==================**######============================##**####==========**##############================######================== 5e ====================================##########== ==========######==================########==========================**########==========##############================**######================== 5f ====================================##########== ==========######========**=======*########========================**########============######==######================######==================== 60 ==########**====================**######========-#**----*########-------================**########============**######====##==============****######==================== 61 ==##########==================**########========-###---**########-------================########==============########====##==========******######====================== 62 ====########**================##########**======--##***#########--------==============**######==****========**######================**############====================== 63 ====##########================##########**======--###*########----------============**########==####**====**########==============**############======================== 64 ======########==================##########======---##########-----------============########======####**==########============**==##############======================== 65 ======########**================##########======---##########-----------==========**######==========####**########============##**######==####========================== 66 ========######**==================########======----########------------==========########==========##############============########================================== 67 ========########==================########**====------######------------==**====**########==========############============**########================================== 68 ========########==================##########====-------#####------------==##==****######==========**##########============**########==================================== 69 ========########====================########====-------#####------------==##**##########==========##########==============########====================================== 6a ==========######**======**==========########**==-------######-----------==############============##########============**######======================================== 6b ==========########======##**==========######**==--------#####*----------==############============########============**########======================================== 6c ==========########======####**========########**---------#####----------==############============######==============########========================================== 6d ==========########======######========##########---------#####----------==##########============**######============**######============================================ 6e ============######**======####==========########*---------####*---------**########==============######==========****########============================================ 6f ============########**====####**========########*---------#####*--------##########==============######========**##########============================================== 70 ============##########****######========#########---------######------**########==============**######====****##########================================================ 71 ==============##################========#########----------#####**---*##########==============######====**############================================================== 72 ==============##################****==**#########**--------#######***#############**========**######****############==================================================== 73 ==============######################**############*--------#########################========####################======================================================== 74 ================##################################----------##################=============*##################========================================================== 75 ---------#################################**========################====--------**############## 76 -----------#################################**====**##############======------**#############--- 77 --------------##############################******################======----**###########------- 78 -----------------#############################**################========---*############-------- 79 --------------------############################################========***#############-------- 7a ---------------------###########################################======**#######-#######--------- 7b ------------------------######################################======**########-*######---------- 7c ------------------------==####################################======########--*######----------- 7d ------------------------====################################======**#######--*#######----------- 7e ------------------------======##############################====**#######---*#######------------ 7f ------------------------========############################====########--**#######------------- 80 ------------------------==========##########################==**######==--#########*------------ 81 ------------------------============########################==########==**###########----------- 82 ------------------------============########################==######====###########------------- 83 ------------------------==============######################**######==**########---------------- 84 ------------------------==============##############################**########------------------ 85 ------------------------================#####################################------------------- 86 ------------------------================#####################################------------------- 87 ------------------------================####################################-------------------- 88 ------------------------==================#################################--------------------- 89 ------------------------==================###############################----------------------- 8a ##############################------------------ 8b -############################------------------- 8c -###########################-------------------- 8d -#########################---------------------- 8e --#######################----------------------- 8f --######################------------------------ 90 ---####################------------------------- 91 ---###################-------------------------- 92 ---###################-------------------------- 93 ----#################--------------------------- 94 ----#################--------------------------- 95 ----################---------------------------- 96 -----###############---------------------------- 97 -----###############---------------------------- 98 -----###############---------------------------- 99 -----###############---------------------------- 9a -----##############----------------------------- 9b -----##############----------------------------- 9c -----##############----------------------------- 9d -----##############----------------------------- 9e -----##############----------------------------- 9f --###############------- a0 --###############------- a1 --###############------- a2 --##############-------- a3 --##############-------- a4 --##############-------- a5 --##############-------- a6 --##############-------- a7 --##############-------- a8 -###############-------- a9 -###############-------- aa -###############-------- ab -##############--------- ac -##############--------- ad -##############--------- ae ###############--------- af ###############--------- b0 ###############--------- b1 ###############--------- b2 ###############--------- b3 ###############---------
Separate hardware sprites are used for the dark grey and light grey parts, but the diagram above only shows the boundaries of the dark grey sprites. To make the graphics, I started with a photo of an apple tree and wrote a program to extract its silhouette and generate a text file in the above format. Then I went over every part of the edge in a text editor, touching up the pixels manually.
Main graphics
Moving on to the snowflakes, we have already deduced that they are emitted by the main graphics generator, but what mode could we be looking at—text or bitmap? Well, there's a lot of movement going on all over the screen, and bitmap mode is generally used for static pictures because there's not enough time for the CPU to redraw the contents of a large bitmap (8 KB) on every frame.
In character mode, we could for instance fill the screen with multiple copies of a 16x16 grid of unique characters (corresponding to 128x128 pixels). By updating only the font definition (2 KB), those changes would affect every copy of the 128x128-pixel template at the same time. However, when we scrutinize this snowfall, it doesn't seem to consist of repeating tiles.
There is however another important clue, quite conspicuous when you know what to look for: The top 12% of the screen is not part of the main effect and is primarily black. To a trained eye, this strongly suggests that the effect involves linecrunch. One of the unforgiving limitations of the C64 video chip, VIC, is that on every video frame, the main graphics generator always starts to read graphics data from the beginning of a designated memory area. Linecrunch is a technique for skipping ahead, advancing a complete text row (eight lines of pixels) on every rasterline. With a series of linecrunch operations, it is possible to nudge the main graphics generator to any desired vertical position in at most 24 rasterlines. So by reserving this much space at the top of the screen (and covering this area with some other effect) the remainder of the screen can be scrolled up or down by any distance. Throw in another trick called VSP, and you can scroll to an arbitrary horizontal position too. The fact that the demo has a configuration menu where you can choose a VSP channel is another clue that this technique is used.
This particular combination of hardware tricks (linecrunch and VSP) is so powerful that it has its own name: AGSP, Any Given Screen Position. But while AGSP allows you to start reading graphics data from an arbitrary address, it does so at the cost of a large part of the screen real estate—that top 12%. This is a high price to pay in text mode, where the grid of characters still visible on the screen would occupy no more than 880 bytes of RAM, little enough for the CPU to update at full frame rate. But when the graphics data is a hefty 8 KB bitmap, the tradeoff suddenly makes a lot of sense. And so we conclude that the snowflakes are displayed using bitmap mode, and that the bitmap data is rendered starting at various offsets.
An oddly-shaped tiling
But the effect certainly doesn't look like a static picture moving vertically and horizontally. So what's going on?
First, let me clarify that bitmap data is confined, at any time, to a designated 8 KB block of memory that always begins on an 8 KB-aligned address. Let's refer to such a memory block as a bank. Furthermore, the pixel data is organised in a peculiar way on the C64: Each 8x8 chunk of pixels (corresponding to a character in text mode) is stored together in memory, as eight consecutive bytes.
Put another way, out of a total of 16 address bits, the top three are directly controlled by the programmer; they determine what bank to access. The bottom three bits identify a particular row within a character; they represent the fine Y position, a small-scale adjustment in the vertical direction, and we can ignore it for the present discussion.
But the middle ten bits determine a coarse position within the bitmap image, or technically within the memory bank where the image is stored. This part of the address encodes both the vertical and horizontal coordinates, baked together as 40y + x:
The video chip tracks the current position with an internal 10-bit register that can only be manipulated indirectly: It is reset to zero at the beginning of a frame, incremented by 40 on a linecrunch, and so on. In the absence of any trickery, the position will advance steadily every eight rasterlines, and by the end of the video frame it will have reached exactly 1000 (40*25 character cells). But when we skip ahead in the sequence using linecrunch, the index can overflow and wrap around modulo 1024.
Again, AGSP lets us start reading the graphics from an arbitrary offset. If we start at offset 5, for instance, the above diagram would be different: The top row would contain boxes 5–44, the second row boxes 45–84, and so on. It would be as though the five leftmost columns had been detached and reattached on the right side, except they would be reattached one box higher up.
In other words, when we start reading data from an arbitraty position in the memory bank, it's as though we're cropping a rectangular piece (320x200 pixels) out of the infinite tiling pattern shown here:

The tiles are non-rectangular because the stride of a line (40*8 bytes) doesn't divide the size of the memory bank (8192 bytes).
2-dimensional zoetropes

A real zoetrope. Photo by Andrew Dunn, CC BY-SA.
But the funny-shaped pattern can be put to good use. Like several effects in my demo Lunatico, this snowstorm is a Wraparound Isometric Zoetrope (WIZ). I named the technique after a mechanical toy from the mid 1800s where animation frames appear next to each other on the inside wall of a wide cylinder. Opposite each frame is a thin slit. By spinning the cylinder and looking through the slits from the outside, you see each frame in turn for a brief moment, and this creates the illusion of animation. As an unintended side-effect, since you can also see through the adjacent slits, you'll see multiple copies of the animation, each at a different offset in the animation cycle.
Suppose we draw a bunch of small animation frames in different parts of a bitmap. By adjusting the scroll offset on every frame, we could bring each animation frame in turn into some part of the screen (e.g. the middle), and thus play the animation there. But the rest of the screen would become a flickering mess of other animation frames.
A more clever approach is to arrange the frames on a diagonal line stretching out across the repeating tile pattern until it eventually returns to the starting point. This results in a kind of 2-dimensional zoetrope, where the same animation will play in several on-screen locations, each at a different offset in the animation cycle. For instance, imagine eight small frames along this line:
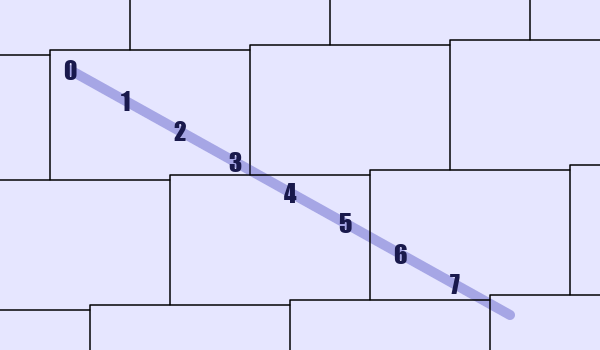
In practice, we draw them in the same bitmap arranged like this:

Now suppose each animation frame grows larger until it starts to interact with its neighbours. At some point we are no longer looking at a set of distinct frames, but rather a single full-screen animation whose individual frames are just rectangular cut-outs at different positions in the tile pattern.
Back when I was working on Lunatico, I discovered a neat twist: It is possible to fit the diagonal line in such a way that the individual animation frames are spread out evenly along both the X and Z base vectors of an isometric 3D coordinate system. But for a 2D-effect like snow, we don't need to bother with that complexity. The only parameter we have to compute is the change in scroll offset from one frame to the next. This determines the length of the animation (the number of frames before the offset wraps back to its initial value), but also where on the bitmap each frame should be drawn. The maximum animation length is 1024 frames, one for each possible 10-bit scroll offset.
Let it snow!
So, let's see if we can put all of this together: A snowflake is an individual animation of a single dot, floating and dancing but generally moving downwards. All of these animation frames are drawn on top of each other in the same bitmap, but at 1024 different offsets. In this way, the final bitmap contains a flurry of snowflakes that are in fact the same snowflake at different times. The whole combined animation will repeat after 1024 frames (about 20 seconds).
In this effect, the snowflake animation actually contains more than 1024 frames, so some of them will be drawn exactly on top of each other in the bitmap, but their dots will be in different places. The scroll offset increases by 595 (modulo 1024) on every frame. The odd number ensures that we'll visit each of the 1024 positions before the sequence repeats. It could have been any odd number; 595 was chosen experimentally, tweaked along with the animation data itself until the snowfall looked good. The tweaking was done while I prototyped the effect in a high-level language on a modern computer. By the time I started to write C64 machine code I already knew that the snowfall would look convincing.
Instead of pre-computing the full bitmap image and including it in the demo, I decided to generate a list of coordinates for each snowflake in animation order. In this way I could introduce the effect gradually by starting with a blank sky and adding one snowflake at a time while running the animation. But the initial part of this fade-in, with only a few snowflakes visible, had a quite regular and unnatural look, so in the end I decided to launch the effect with several snowflakes already in the air. You can still see a gradual increase just after the demo starts.
If the snowflake animation involves a general downwards movement, it can't be cyclic; the snowflake has to appear out of thin air, fall for a while, and then disappear. Won't this look weird? As it turns out, a snowflake appearing out of thin air is no problem, but its disappearance can be a bit jarring. This is probably because the eye will lock on to a snowflake and follow it, and notice when it suddenly disappears—but the eye rarely happens to be looking at the spot where a new snowflake appears. To get around the problem of the abrupt disappearance, observe that as more and more snowflakes are added to the bitmap, they will eventually start to run into each other. I simply end the animation at one of the points where the snowflake coincides with another copy of itself. On the screen, it looks like two snowflakes merge into one, and this is inconspicuous enough that you're unlikely to notice it.
Through the looking-glass
So far we have seen how the snowfall is animated; all the frames are drawn on top of each other, overlapping, across a static bitmap. But there's a complication: This effect depicts a window, looking out over a snowy landscape, and the window is frosted along the edges. But because of the candlestick and the trunk of the tree, we only have six out of eight sprites left to draw the frost along the bottom edge. Six X-expanded sprites will only cover 288 pixels out of 320 (corresponding to 36 characters out of 40). In other words, the window cannot be as wide as the screen. But the bitmap is a homogeneous field of snowflakes, extending in all directions. How do we prevent snowflakes from showing up along the left and right edges of the screen, outside the window frame?
In hi-res bitmap mode, the foreground and background colour of each 8x8 chunk of pixels is determined by a byte in the so called video matrix, a separate 1 KB memory bank. For a full-screen snow effect, we could keep this matrix filled with a single value that selects a white foreground (for the snowflakes) and a medium grey background (for the sky). To limit the display to a subsection of the screen, we simply set both the foreground and the background to black in the cells outside the desired area.
But there's a snag: The linecrunch and VSP effects affect the index into both the bitmap and the video matrix at the same time. Thus, our black stencil would stick to the bitmap, jumping wildly across the screen as we update the scroll offset. We'd have to compensate for this, and redraw the contents of the entire 1 KB video matrix for each frame, at an offset that exactly cancels the AGSP.
There are two problems with this approach. One is that the last eight bytes of a video matrix bank also serve as sprite pointers that determine where to fetch the pixels for each of the eight sprites. Normally, the main graphics generator only looks at the first 1000 bytes of the video matrix, so these eight bytes are out of the way. But since we use linecrunch to skip ahead to an arbitrary offset, the eight bytes may have to perform double duty as colour information and sprite pointers. The workaround is to perform perfectly-timed bank switches, so the main graphics generator reads from one 1 KB bank while the sprite pointers are fetched from another.
But the other problem is that we don't have enough CPU cycles left to update 1 KB on every frame, considering all the other timed trickery we have to perform. The solution to both problems comes in the form of another VIC hack: Normally on every eighth rasterline, VIC pauses the CPU for 40 cycles in order to read new data from the video matrix. This is known as a badline because it interferes with timed code. But we can trick the VIC chip and inhibit all the badlines, one at a time, using timed writes to the hardware registers. The video matrix data from the first line will then be repeated throughout the display.
In this way, we only need to prepare one row of video matrix data: 40 bytes starting from the current AGSP scroll offset. The first two and last two of these bytes should select black-on-black and the middle 36 should select white-on-grey. This pattern will repeat vertically, forming solid black columns along the left and right edges of the screen. The downside is that we need to perform timed register writes regularly throughout the entire video frame in order to inhibit badlines, but on the other hand we regain all the clock cycles that would otherwise have been stolen from the CPU. We still need to perform a perfectly-timed bank switch in case our 40 bytes overlap with the sprite-pointer area, but we only need to do this once per frame.
A busy schedule
Finally, the scroller over the linecrunch area consists of six X-expanded sprites whose contents are updated in software. With that I think we've discussed every part of the visuals.
On the whole, this effect involves plenty of timing-critical code. The eight hardware sprites are reused several times per video frame, but due to the irregular shape of the tree they are not all active at all times. The CPU is stalled when sprite data is fetched too, so the end result is a very complicated puzzle of timed register writes that influence the timing of subsequent code. It is possible to program an effect manually under such conditions, but this takes a lot of work, and as a consequence one tends to avoid changing any instructions that have already been laid down.
To give myself the freedom to move things around (such as the tree and candle graphics) and try out different options, I decided to write a code-generator for the timed parts of the program. The generator runs at compile-time. It knows about all the stolen clock cycles, based on the sprite positions that I declare. I also specify a set of code snippets, each with a constraint to execute at a particular clock cycle, or within a range of clock cycles. The generator finds a place in the schedule for each snippet and fills the rest of the program with no-operation instructions. The scheduling is performed using a primitive greedy algorithm, so this is really only a semi-automated system. But it's been extremely useful as a tool to help me juggle all the bank switches, sprite parameter updates, and inhibited badlines while being able to tweak and experiment with the visual appearance.
Rounding it off
One more thing: The scroll text claims that we're looking at 1156 dots. Where does that figure come from? The actual snowflake animation happens to contain 1496 frames. It ends at a point where the snowflake coincides with an earlier copy of itself on the bitmap, as discussed previously, but there are many such occasions and I just picked an animation length that made the snowfall look good—dense but not overcrowded. The linecrunch area and the blacked-out edges cover approximately 20% of the bitmap, which leaves about 1200 dots in the visible area at any given time.
But by quoting a specific and vaguely technical-sounding number like 1156, I'm suggesting that the number of snowflakes is significant and somehow directly related to the difficulty of implementing the demo part. This is an attempt to throw the audience off the scent about how the effect really works. And thus we top off this rather technical magic trick with a bit of classic misdirection.
Posted Wednesday 15-Feb-2023 21:20
Discuss this page
Disclaimer: I am not responsible for what people (other than myself) write in the forums. Please report any abuse, such as insults, slander, spam and illegal material, and I will take appropriate actions. Don't feed the trolls.
Jag tar inget ansvar för det som skrivs i forumet, förutom mina egna inlägg. Vänligen rapportera alla inlägg som bryter mot reglerna, så ska jag se vad jag kan göra. Som regelbrott räknas till exempel förolämpningar, förtal, spam och olagligt material. Mata inte trålarna.
Thu 16-Feb-2023 04:29
Sun 19-Feb-2023 11:40


